Solving a Sudoku, part I.

Gam3s Comments Off

May 112011

Solving ways

Everyone’s having his own way of solving a SuDoku, some people add tons of mathematics and ruin all the fun, others start guessing randomly and make a mess, and some make it to an unknown algorithm just by trial and error 😉 I hope that sharing my few SuDoku solving ways will help you do better, even if you are tournament winner, geek mathematician or a ordinary guy with free time and a newspaper.

Some dry theory

The Japanese 数独 is actually spelled “Kazu Doku”. Not sure about the exact translation but Kazu is translated as Number and Doku as Single. If we want to say “Single number” by those two hans, the sentence would sound as SuDoku as possible. If you look at the grid, every 3×3 square, every column or every row should have only one (single) digit in the range 1-9. (If you know better translation and meaning of the word SuDoku – feel free to comment) 1 game grid has 9x3x3 squares which form 9 columns and 9 rows. That’s all the actual game rules provided by Nikoli magazine that originally developed this puzzle game in 1986. Strangely, not many people know them outside Japan. If you are dedicated SuDoku fan, I suggest you pay a visit to their online magazine and get more good ideas and puzzles.

Considering the numbers set on the grid, we can tell if SuDoku is easy, normal, hard, very hard or Impossible.

Easy grid

Easy grids are having almost half of the numbers filled, with 3 to 5 numbers in any 3×3 grid.

Normal grid is having 28-35 numbers with at least 3 numbers in any 3×3 grid.

Hard are the grids with 25-30 numbers leaving every 3×3 grid with 2 to 4 numbers.

Very hard are the grids with 22-24 numbers. In practice, that means every 3×3 square will have zero or up to 3 numbers inside.

Less than 22 numbers on the grid is practically having more than 1 solution, so it’s “Impossible” to be done without pencil and some preparation.

Further, I call plane any 3 horizontal 3×3 grids, (e.g. top, middle and bottom plane) and pillar any 3 vertical 3×3 grids (e.g. left, middle and right pillar). Of course – feel free to call them whatever you like. Wikipedia article calls the 3×3 grids “areas”, so we can also adopt this slang for the text below.

Simple method (a.k.a. baby steps)

Middle plane of the above grid

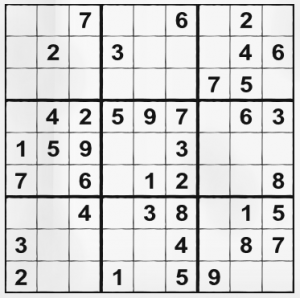
It is applicable for easy and some normal grids only. You start searching one by one all 3×3 squares for any easy numbers. Also one-by-one. e.g. Where can 1 be put according to the positions of other “1” digits in the grids and the rows around this 3×3 square. If you can’t find any digit’s position, you go to the next until you finish all 9 and return to the first. We are not robots of course. If you have a look at the grid above, you can easily see that starting from the beginning is pointless, because the grid has less numbers in top plane and lots in the middle plane. Observing left 3×3 area of middle plane, we can easily deduct that numbers 3 and 8 are missing. We put 8 in top left, because 3 can’t stand there (have a look at most right number in row 4) than we put number 3 in the other left square, because that’s all that is left. One area is filled. The middle area is unsolvable by this easy method – missing numbers 4, 6 and 8 are no where to be found in the near vicinity. Rightmost area of middle plane is missing the numbers 1, 2, 4, 5, 7 and 9. All of them – very easy. 1 is the only missing number in row 4, the middle square is the only that can hold 7 (see around), bottom left is for 5, and bottom middle is 9. The 2 numbers left we abandon for now (2 and 4). We keep that up, until we cover all easier areas and than go to harder ones. Takes about 2 minutes of trained eye to solve easy and normal grids.

“Dim view” method.

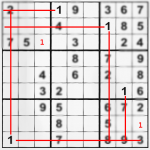
If you are using some online SuDoku client, you probably have a tool that does the same. If you are in front of the newspaper, you probably don’t :D. This method, as funny as it sounds is very useful for people with good photo memory. Regardless the funny name I’ve put – It’s one of the fastest ways to find numbers in hard grids. Why am I calling it “Dim view“? Try to look at the grid and focus your eyes on one number only. The other appear a bit dim ;). With this focus you can easily see where a number can and cannot be. (see the pictures below). A trained “dim” eye can spot in one easy cycle the places of most numbers for less than a minute.

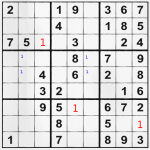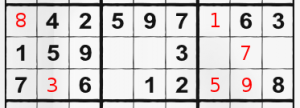
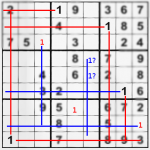
“1” can be put at top left area and bottom right area easily, because that’s the only position’s left for it. And having a second glance – another “1” can be put in the middle area of bottom plane after we put the two “1” numbers on the grid and having them in mind. Finally, you have 3 number “1” positions (red) and 2 number “1” probable positions (blue). If you continue using this method for all digits, you will see that 2 and 3 are unsolvable in this easy way. On the other hand the number “4” covers all the grid and the 2 number “1” we put with pencil (see the blue digits above) can be put with pen, because one of the “4” is ruling their exact places out. Number “5” is very easy, leaving only 2 areas unsure. “6” has only one possible position, so we quickly abandon it. “7”, “8” and “9” are another very easy grid-fillers. All that is left are … few baby steps, to complete the whole grid. It is very easy now to find the missing places of “2”, “3” and the few “5” missing.

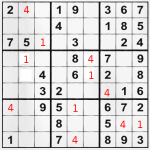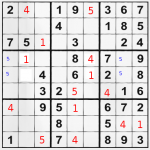This method is a lot faster than the previous, because it solves all 9 areas for less time and gives you better perspective what and where is missing. It’s not very applicable for all hard grids and is not very good for very hard and impossible grids. I still use it on harder grids, to see if there is good “weak spot” or “weak number” to cover it for few seconds at a glance. For harder grids, you have to look part II of this article.

Mythos

Gam3s 1 Response »

May 052011

Mythos Europe logo

I was amazed to see, that the game is actually already online. Was hearing rumors, that the team that left Blizzard North to start a new company named Flagship studios has declared bankrupt and abandoned the title. For some reason, while watching my own blog from my work PC for defects and glitches (don’t tell my boss 😉 ) I spotted an Advertising below the menu, claiming Mythos is already playable (closed beta is over).

I almost clicked my own Ad unit, which is actually forbidden by Google and may ban my Adsense account 😀

Anyway. First impressions.

The game is still very young. The servers are not very populated yet, but even so the developer team has implemented “rooms”, so If you are hunting in a full room, you may switch to an emptier one. For solo-lovers like me, this is very good. Even with young server population, we already see few capped heroes (5 days since start) so I suppose, this game will be more Blizzard-like than the other free-to-play MMORPGs around the globe. That means, the build should be all basic and straight forward to be made and EVERYTHING will be based around how good is your equipment. At least everyone in the Forum that reached level cap claims “It’s extremely boring” after this and all you have to do is hunt better equips and make money for your alt characters. (check the forum)

The 3D view may benefit from some fixes. The isometric 3D view is fine. The free view (MMO style) is badly implemented though. The same left mouse button is used to move/attack and for free-rotate too. Because of this, you often think you clicked on a monster, while actually you rotated your view. Also, you may rotate to such angle, that you actually look very … intimately … closely … near … at your hero’s a$$. In hack and slash games like this, few seconds of tinkering with your mouse to reposition your view can be critical. So I quickly abandoned the free 3D view and turned to isometric.

Intuitive controls. WASD + mouse. Every letter you used in Diablo II does the same here. The new stuff is World map, accomplishments Journal and Crafting. Enough said.

Three stream of classes. Thug, mage, mechanic. All of them has 3 main subclasses, which can be combined between (a.k.a. builds) in a way, that you may choose skills from all 3 subclasses or focus on a single one. Playable races. Elven, Cyclops, Human and Satyr. All four has their own pros and cons. Elves are cute, small, accurate. Cyclops are strong brutes with more armor and endurance. Humans are high HP jack-of-all-traders. And Satyrs have most MPs of all classes. To mix all this is to have (4 rases x 3 classes x 3 subclasses) 26 possible combinations of the pure builds. (e.g. every Cyclops Bloodletter will have 3 pure builds, every Gremlin Pyromancer too and so on).

On every level up (Level cap is 50) you receive 2 skill points, 5 stat points and 2 craft points. So far if there are no quest that give few point to this or that – those point are enough for … nothing. You make some points to Str and Vit so you can equip the stuff you will need and focus on pure Strength, Dexterity, Vitality or Spirit. There is another stat called Luck, which is not advanceable by leveling up. Equipment only.

The source of all evil.

Money. 100 copper = 1 silver, 100 silver = 1 gold, (and maybe 100 gold was 1 of whatever this in the left looked like, but they removed it already). The trade system is like WoW. You get your stuff into the market list and set start bid and final price. Basically, the good stuff can be started @ 10 to 20 times the NPC price. At least the good yellow (unique) ring goes in 10 minutes for 20 times the NPC price and level 15 hero can get 1-2 unique drops by quests only, so it’s not constant grinding for money. If you succeed in selling, you receive your money by mail 😀 while grinding in the deepest dungeon with 5% tax deducted. Much different from Fiesta online or Maple Story’s casual shop, where you have to stay online in the market until trading.

There is also no censoring 😀

There are some nasty bugs, like “you can’t shoot monsters laying in your feet”. You kill everything else with ease, but the monster that is in same XY coordinates as you – totally invulnerable to shooting. Grenades work though. Hope they fix this soon or add “kick” skill :D. The Free-MMO-like-3D view is a bad experience also. Some quests description is inaccurate, misleading or not translated good. E.g. “I’ve spent all my craft skills for BS and still can’t get a quest done, because it says Heraldry level above 2, then not explaining WHICH skill exactly you should rise to reach this level”. Hopefully and thankfully there is NPC that resets skill points (a.k.a. respec) and this will not be fatal. Sorry to say, the Stats can not be reset and if you choose to focus on STR, DEX or WIS – you stick with this for the chosen build.

Grinding barrier is reached normally after ~ 4-5 days of playing and starts at level 21. Quests are not enough to proceed leveling by them and you have to grind. The best place for grinding is … ahem … FAP, 😀 accessible from Crumbled Kingdom and there are often parties of 3-4 people collecting more for entering FAP instanced dungeon.

Server maintenance. Thursday. Really annoying. The same day as most of the other free MMORPGs around. I was hoping to play this game when Fiesta Online is down for maintenance. Hopefully Maple Story will keep their maintenance @ Wednesdays for the time being.

How to find the IP address of Skype user

Netw0rking 14 Responses »

May 042011

I’ve seen this question on several forums around the globe.

Most of the answers were “You can’t”

Strange.

You actually really CAN’T. From Skype :D. But Skype is solely based on P2P connections and you can’t connect to any peer if you don’t have/know his IP address. They simply refuse to disclose their protocol for the public, so we can write our own plugins for Skype.

So, I’ve just had a look at my netstat output (Linux console, sorry – for Windows read below):

bash-4.1# netstat -tupan | grep skype
tcp        0      0 0.0.0.0:20530           0.0.0.0:*               LISTEN      2081/skype         
tcp        0      0 10.3.71.55:38804        212.75.19.204:6521      ESTABLISHED 2081/skype         
tcp        0      0 10.3.71.55:58519        93.152.140.108:23669    ESTABLISHED 2081/skype         
udp        0      0 127.0.0.1:59356         0.0.0.0:*                           2081/skype         
udp        0      0 0.0.0.0:20530           0.0.0.0:*                           2081/skype         
bash-4.1#

And then I’ve talked to one of my colleagues in office via Skype and rechecked for any new connections:

bash-4.1# netstat -tupan | grep skype
tcp        0      0 0.0.0.0:20530           0.0.0.0:*               LISTEN      2081/skype         
tcp        0      0 10.3.71.55:38804        212.75.19.204:6521      ESTABLISHED 2081/skype         
tcp        0      0 10.3.71.55:58519        93.152.140.108:23669    ESTABLISHED 2081/skype         
tcp        0    272 10.3.71.55:55886        10.3.71.97:16592        ESTABLISHED 2081/skype
udp        0      0 127.0.0.1:59356         0.0.0.0:*                           2081/skype         
udp        0      0 0.0.0.0:20530           0.0.0.0:*                           2081/skype         
bash-4.1#

See the 5-th line? There are too many lines, you may take the output in 2 files and then use diff.

bash-4.1# netstat -tupan | grep skype > file1.txt
bash-4.1# netstat -tupan | grep skype > file2.txt
bash-4.1# diff file1.txt file2.txt

Than I checked my own IP address:

bash-4.1# ifconfig | grep "addr:"
 inet addr:10.3.71.55  Bcast:10.3.255.255  Mask:255.255.0.0

Obviously my colleague’s IP address is 10.3.71.97.

It’s as easy as this in Windows actually. You only need to enter the Command prompt (Start -> Run -> cmd) and enter netstat the same way as with Linux (don’t know about the options after the dash and you will not have grep and protocol resolution). The Skype connection port is varying every time, so you may be in a bit of an analyze, but basically it’s the same. Your own IP address can be seen if you enter the command ipconfig /all:

If you are really LOST in CMD mode. Try this little nifty program from Windows SysInternals. It’s doing it’s job splendidly. Just don’t forget to use the sort and filter functions if you happen to have too much connections with your PC. The principle is the same.

That’s basically all. Remember your IP address (see above) Talk in Skype to the person for which IP address you are interested and watch the new connection Skype opens. Voila. The IP address is there.

All of this will not happen if the person in you are interested is using Proxy or any anonymizer software. Then you will see random Proxy address. And to try to hack a proxy server is not something that you will just find out by reading blogs and forums. Also, there is some chance that Microsoft will change part of the Skype protocol. Good luck. 😉

There are a lot of attempts to crack Skype protocol, all of them in vain. Perhaps some day the protocol will be reverse engineered and Skype security will not be so tight. There are rumors of ONE person who did this and got a nifty $um of money for his silence.

Anyway. Feel free to bridge your Skype connection over a sniffer and try your luck. I cannot teach you how to disassemble the Skype protocol.