Slackware has one of the most easy to install and setup TFTP servers around. It’s really simple. That’s what you do in a nut shell:
su wget ftp://ftp.slackware.com/pub/slackware/slackware-current/slackware/n/tftp-hpa-0.49-i486-1.txz installpkg tftp-hpa-0.49-i486-1.txz echo "tftp dgram udp wait root /usr/sbin/in.tftpd in.tftpd -s /tftpboot -r blksize" >> /etc/inetd.conf mkdir /tftpboot chmod +777 /tftpboot chown nobody /tftpboot touch /tftpboot/test.txt echo "blah blah blah" >> /tftpboot/test.txt /etc/rc.d/rc.inetd restart tftp 127.0.0.1 -c get test.txt cat test.txt
That will do the job most quickly [and a little bit risky]. If you need the above gibberish explained, that’s what happens:
su
You need to be root or super user to install packages and setup configuration files in /etc directory.
wget ftp://ftp.slackware.com/pub/slackware/slackware-current/slackware/n/tftp-hpa-0.49-i486-1.txz installpkg tftp-hpa-0.49-i486-1.txz echo "tftp dgram udp wait root /usr/sbin/in.tftpd in.tftpd -s /tftpboot -r blksize" >> /etc/inetd.conf
Those few lines will differ a bit in other/older/newer versions of Slackware Linux, but basically, they get the package, install it and setup the tftpd daemon to start at boot time with some important parameters. If you already have the package installed, the wget and install can be skipped. The echo line in the end is quite insecure, so it’s better to open the configuration file and uncomment it’s own config line (remove the pound sign in the line beginning with #tftp dgram udp). That’s the right way to do it, if you are not in a hurry, because the command shown here will add another line in the file. No one can guarantee us, there is no such line in the file already and no one can tell if the parameters are not going to change in future version or are supported in older version. If you know what this line is actually doing – feel free to copy and paste everything. It’s enough. (If you want to know what it actually does – it starts tftpd listening on UDP port 69 for tftp commands as a root user, puts it to silent mode and operates in directory /tftpboot)
mkdir /tftpboot chmod +777 /tftpboot chown nobody /tftpboot touch /tftpboot/test.txt echo "blah blah blah" >> /tftpboot/test.txt
We create the directory, change it’s ownership to nobody and make it accessible to everyone. Than we create a test file and fill in some text which we will use for 
/etc/rc.d/rc.inetd restart tftp 127.0.0.1 -c get test.txt cat test.txt
We restart the internet super daemon and get the file we created via tftp protocol. And just in case, we check if we got the file with the line “blah blah blah” inside in the current directory where we just downloaded it.
That’s all there is for this TFTP server. Quick and easy.
Short disclaimer: Suitable for all simple uses as getting configuration files or boot images on Cisco/Telco/Extreme and other units I have not used. Also not setting any actual securities, so if you are paranoid slacker – this article is not for you. Google for some more extensive guide.


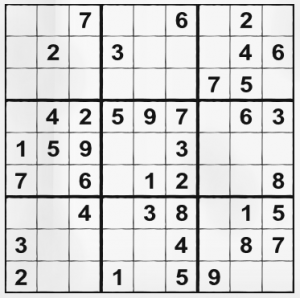
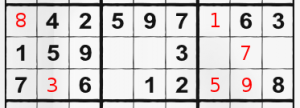
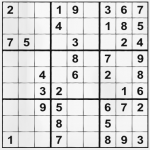
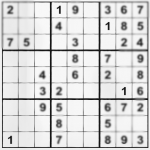
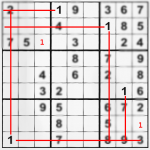
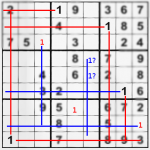
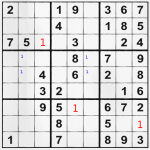
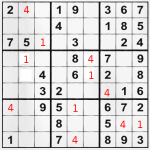
 I hope that sharing my few SuDoku solving ways will help you do better, even if you are tournament winner, geek mathematician or a ordinary guy with free time and a newspaper.
I hope that sharing my few SuDoku solving ways will help you do better, even if you are tournament winner, geek mathematician or a ordinary guy with free time and a newspaper.