Solving a Sudoku, part II.

If you are unfamiliar with the game, or this method is a bit advanced to you – please see my previous article about the 2 basic methods.

If you try to solve this grid by using the “Dim view” you will go almost nowhere. You will find some of the probable number positions and few exact positions. Of course, we feel lucky, and we may try.

This method is a bit more hard, I call it

Blocked squares

If you start using baby steps or dim view on this grid, you will end up with a grid filled with pencil scratches, some of them very useful, and some of them completely useless, until late game. You should of course, always give it a try with simpler and faster methods and then introduce some logic. The very basic trade of this method is to sweep a hard or very hard grid and point the possible numbers in any 3×3 area so you can block some of the squares inside.

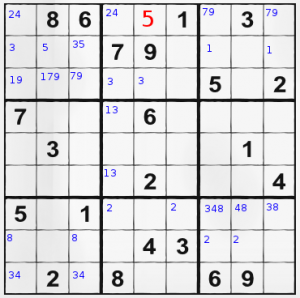
Having a look in this scratched-a-bit grid on right, you will easily notice that left area of top plane has its bottom 3 squares with only possible numbers 1, 7 and 9. Rightmost area of same top plane has above 2 missing numbers either 7 or 9. Both of those areas leave us with some 4 more squares to guess, and some of those 4 squares are half solved.

Middle area of middle  plane has 2 blocked squares with either 1 or 3.

Bottom plane has it’s bottom left area with blocked numbers 3 or 4 and rightmost top are with line filed with 3, 4 or 8.

This is not really helping much by first glance, but let’s repeat the procedure again and recheck this time only the areas with some blocked squares by baby steps, number by number. Having this passed again, you find, that the bottom plane has number 2 in 4 possible positions. Write them down and don’t mess with this method anymore for now, but keep it in mind for a bit later. It’s useful to have a pencil to write probable numbers, before making them with a pen. If you use pen directly, you may get the stuff wrong.

Lines and crosses

If you look at the grid above you will see it’s really going to fit in category very hard. It has only one possible solution, and it is suitable to explain  this method, because the 3 method explained so far … fail to make any number to it’s place. The name of the method explains almost everything. We find a line that has more than 3 numbers in it and try to build up from there.

Having a look at all the candidates in the grid with all the blocked squares, few things pop up.

• There are rows with more numbers either written or probable.
• There are columns with more numbers either written or probable.
• There are crosses formed from those rows and columns.

What does that mean? Probably some easy numbers will pop up 🙂

Have a very careful look at topmost row 1. We have the following: X,8,6,5,5,1,7/9,3,7/9. 4 known numbers. 2 blocked squares. 2 positions with probable 5’s and one completely unknown. Missing numbers 2 and 4. Now we have a look at the numbers below. First square of this row can hold only 2 or 4 and 4-th square of the same row can also hold only 2 or 4 (have a good look at the columns). This leaves one of the squares with probable 5 obsolete and the next square beside it – absolutely certain. Can hold 5 and nothing more, because the other 2 missing, non-blocked squares will hold 2 or 4 and this exact square already has the numbers 2 and 4 in the 5-th column, so they CAN’T stand there.

Congratulations, we have the first number. We write it down and tap our shoulder proudly.

This one is particularly hard. It took me 1 (one) hour and I have made 4 errors. Will leave it this way, so you try your luck 😉